Andrew Ng 교수님의 Machine Learning Specialization 강의를 정리한 내용입니다.
Coursera가 아닌 네이버 부스트코스에서 제공하는 버전을 수강하고 있습니다.
Neural Network를 프로그래밍으로 구현하기에 앞서 어떤 방식으로 구현할 수 있는지 알아보는 챕터입니다. Training 데이터를 for문을 통해 한줄한줄 들여다 보는 것을 추구하지 않기 때문에 Neural Network의 계산 방식인 역전파(backward propagation), 순전파(forward propagation)은 어떻게 구현되어 있는지 살펴볼 것입니다. 그리고 역전파, 순전파의 이해를 돕기 위해 logistic regression을 먼저 살펴볼 것입니다.
이진 분류
Logistic regression은 이진 분류(binary classification)을 위한 알고리즘입니다. x 입력값인 이미지 한장을 보고 고양이면 y 출력값으로 1, 고양이가 아니면 y를 0으로 판단하는 것이 대표적인 예시입니다. 입력값 x는 픽셀들로 이뤄져있고, RGB 값을 각각 가집니다.

입력값 x를 feature vector로 풀어서 작성하면 다음과 같이 표현할 수 있고, 값의 갯수는 64*64 픽셀로 가정했을 때 3개의 채널까지 곱해 12,288 차원인 것을 알 수 있습니다.

입력값 x, 출력값 y를 (x, y)로 표현하고, x는 실수이며 y는 0 또는 1의 값을 가집니다. 개별 x와 y에 대해서는 윗첨자로 인덱스를 의미하는 i를 올려줍니다. 그리고 데이터 (x, y)의 전체 갯수는 주로 m으로 나타냅니다. 표기법은 수식으로 쓰기에 귀찮으니 필기 이미지를 붙여오겠습니다. 알아보기 약간 힘들지만, Andrew Ng 교수님의 글씨체를 잘 따라했다는 생각이 듭니다.

위 표기법을 이용해서 단일 x와 y의 집합인 전체 X와 Y를 표현하면 다음과 같습니다.


그리고 이번 단원의 최종 목표는 프로그래밍을 해보는 것이므로 차원값을 Python에서 불러오는 .shape 까지 확인하고 갑니다. X.shape 를 출력하면, $(n_x, m)$ 이고, Y.shape를 출력하면, $(1, m)$ 이 나오게 됩니다.
Logistic Regression
지도학습(supervised learning)에서 y를 0과 1로 분류할 때 사용하는 알고리즘이 logistic regression입니다. x가 주어졌을 때, $\hat{y}$을 구하는 것입니다. 앞선 예시와 마찬가지로 이미지가 고양이이면 1로 표시할 경우, 이미지가 고양이일 확률을 수식으로 표현하면 다음과 같습니다.
$$ \hat{y} = P(y=1 | x)$$
계산을 위해 logistic regression을 수식으로 표현하고자 합니다. Binary classification을 위해 출력값 y가 0과 1 사이 값을 가지는 함수는 sigmoid 함수입니다.
$$\hat{y} = \sigma(w^Tx+b)$$
$$z=w^Tx+b$$
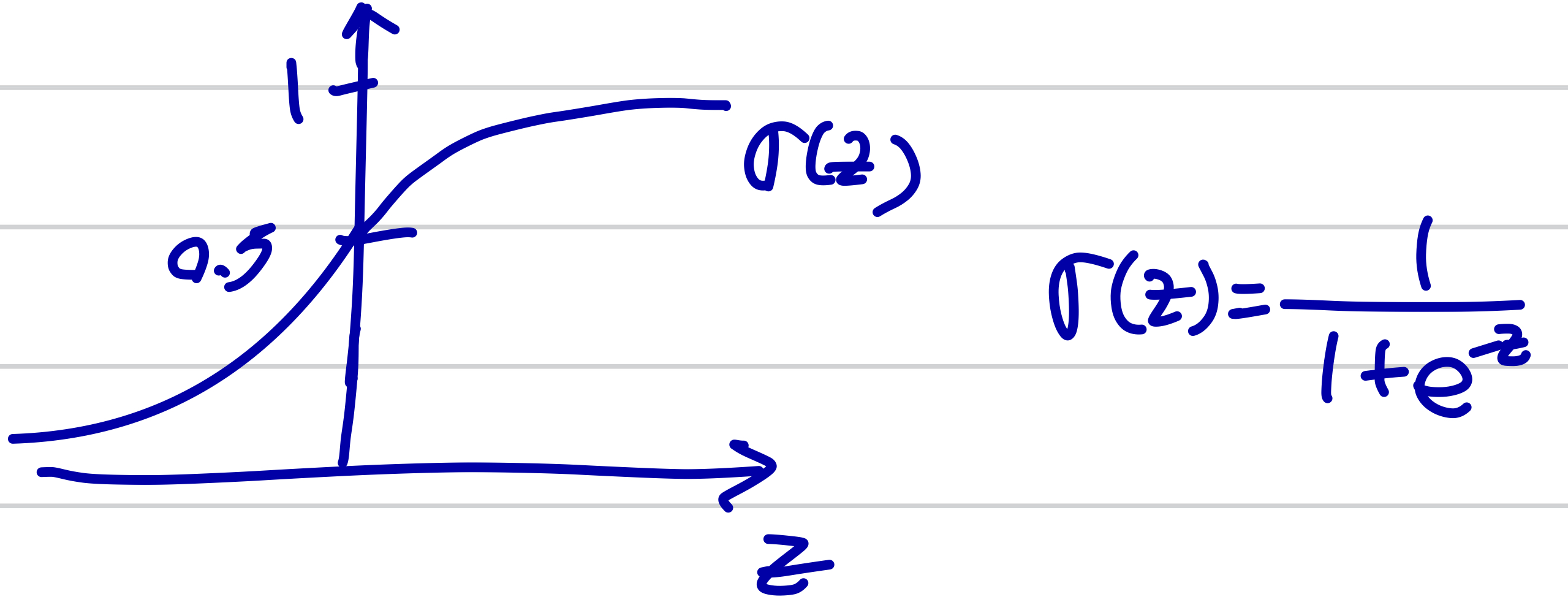
z값이 크다면, 1로 수렴하겠고, z값이 작다면 0으로 수렴하는 형태를 보이기 때문에 logistic regression을 표현하는 데에 사용하게 되었습니다.
Logistic Regression Cost Function
Logistic regression 수식에는 w,b 매개변수가 있고, w,b 값을 학습하기 위해 cost function이 필요합니다. 단일 x와 y에 대해서 ground truth y와 $\hat{y}$ 값의 차이를 loss function이라고 합니다. Loss function은 직관적으로 생각했을 때나 앞서 배운 linear regression에서 계산한 바에 따르면 다음 식과 같습니다.
$$ L(\hat{y}, y) = \frac{1}{2}(\hat{y}-y)^2$$
그러나 logistic regression에서는 해당 loss function을 사용하지 않습니다. 볼록함수(convex function)이 아니기 때문에 global minimum을 찾지 못하기 때문에 gradient descent를 통해서 local minimum 값 밖에 찾을 수 없다고 합니다. 따라서 다른 사람들이 convex한 다른 loss function을 찾아 놨습니다.
$$L(\hat{y}, y) = -(y\log \hat{y} + (1-y)\log (1-\hat{y}))$$
y = 1: $ L(\hat{y}, y) = -\log\hat{y} $
y = 0: $ L(\hat{y}, y) = -\log(1-\hat{y}) $
y가 1이면, $\log\hat{y}$이 커지는 것이 loss를 줄이게 되고, $\hat{y}$ 값이 커지게 해야합니다.
y가 0이면, $log(1-\hat{y})$ 이 커지게 만들어야 하므로 $\hat{y}$ 값은 작아지게 만들어야겠습니다. 그러나 y=1, y=0 인 경우를 설명한 것은 직관적으로 loss function을 이해할 수 있게 설명한 것이고 사실 y값이 커져서 loss를 줄일 수 있는 함수는 무궁무진하게 만들어낼 수 있겠죠. 아무튼 결론적으로 우리는 0과 1 사이의 $\hat{y}$을 가지고 loss를 최소화해야 합니다.
Loss 는 단일 데이터, 하나의 $\hat{y}$에 대해서 이야기 했다면 cost function은 전체 훈련 데이터셋에 맞춰 parameter가 적은 cost를 가지는지 즉, 얼마나 잘 예측되었는지 판단하는 함수입니다.
$$J(w,b) = \frac{1}{m} \sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) $$
$$ J(w,b) = -\frac{1}{m} \sum_{i=1}^{m}[\log y^{(i)} + (1-y^{(i)} \log(1-\hat{y}^{(i)} ]$$
Logistic regression은 작은 Neural Network 이다. -Andrew Ng 교수님의 한마디-
Gradient Descent
그럼 본격적으로 cost function $J(w,b)$를 가장 작게 만드는 w,b를 구해야 합니다. Gradient Descent 경사하강법을 이용해서 J(w,b)의 최저점(global minimum)을 알아냅니다. Logistic regression의 경사하강법에 대해서는 앞선 코세라 강의에서 이야기 나눈 바 있습니다.(Machine Learning Specialization Week3. Lesson3 참고: 링크) 이번 강의에서는 이전보다 더 자세하게 편미분에 대해서 이야기 합니다. w값을 업데이트 할 때에는 w에 대해서만 미분한다 = w에 대해 편미분한다. 편미분되는 미분 계수는 cost function의 J(w) 기울기이고, $\alpha$ 값은 얼마나 기울기 하강을 진행하는지 나타내는 learning rate입니다. 다음처럼 w에 대한 값 갱신(update) 식을 정할 수 있습니다.
$$ w = w - \alpha \frac{\partial J(w)}{\partial w}$$
Computation Graph
Neural Network의 연산을 알아보고자 합니다. 연산은 크게 두가지로 생각할 수 있습니다.
- Forward propagation(순전파): Neural Network의 출력값 계산
- Backward propagation(역전파): 기울기(gradient), 도함수 계산
Neural Network 연산을 그래프를 통해서 그리는 연습을 해볼 것입니다.
$$J(a,b,c) = 3(a + bc) $$
위와 같은 cost function을 computation graph로 그려보았습니다. 값은 Andrew Ng 교수님이 들은 예시로 빨간색으로 작성하였습니다.

a 값의 변화가 J(a,b,c)에 어떤 변화를 일으키는지 알아보려고 합니다. 변화량은 미분값이므로 미분을 이용해서 아래 식으로 표현 가능합니다.
$$\frac{d J}{d a} $$
a에 0.001 증가라는 작은 변화를 일으킨다고 하면, J는 0.003 증가가 발생합니다. 지금은 식이 간단해서 바로 암산이 되었을지 모르겠지만, 자세히 풀어쓰면 a 변화에 따른 v의 변화량, v 변화에 따른 J 변화량을 곱한 값으로 계산한 겁니다.(그렇다고 해!) 이는 chain rule 을 기반으로 계산된 겁니다.

여전히 이번 단원의 최종 목표는 프로그래밍을 해보는 것이므로 분수로 표현된 미분값을 Python으로 변수는 dJ, dv로 지정할 것입니다.
$$\frac{dJ}{d a} => da$$
이를 규칙으로 만들었습니다. F final output var은 보통 cost function J가 됩니다.

$\frac{dJ}{dc}$ 를 계산하고 싶다면, 아래 풀이대로 계산할 수 있습니다. 여기서 중요한 점은 도함수 계산을 위해서 파란색 화살표처럼 오른쪽에서 왼쪽으로 미분 계산을 했다는 점입니다. v에 대한 미분, u에 대한 미분, c에 대한 미분을 차례대로 해야 구할 수 있습니다. da, db는 Andrew Ng 교수님이 영상에서 진행했으니 참고 바랍니다.(Derivatives with computation graphs: 링크)

Logistic Regression Gradient Descent
Logistic regression의 경사하강법을 위에서 배운 computation graph로 진행해보려고 합니다. 연습을 위해 logistic regression의 경사하강법에서 진행되는 미분 계산을 위에 a,b,c 예시와 동일하게 생각하면 됩니다.
앞에서 살펴본 logistic regression에서 사용하는 수식들을 나열해보겠습니다.
$z=w^Tx+b$
$\hat{y} = a = \sigma(w^Tx+b)$
$L(a, y) = -(y\log (a) + (1-y)\log (1-a))$
이 식을 위에서 본 computation graph에 대입하고, 미분값까지 계산하면 아래와 같이 정리됩니다. 제가 아주 이쁘게 꾸며봤습니다. a-y가 왜 나온 것이냐면 $da\cdot dz$ 값을 계산해서 나온 것인데, $da$ 는 연두색 박스한 것과 같이 오른쪽에서 먼저 미분한 값이 있기 때문에 결과가 나올 수 있었습니다.

위 계산 결과를 기반으로 단일 샘플에 대해서는 파라미터를 업데이트할 수 있습니다. 마지막 파라미터 값 $w_1$, $w_2$, $b$에 대해서 미분을 한 번 더 진행하면, 다음과 같이 나옵니다.
$$ \frac{\partial L}{\partial w_1} = dw_1 = x_1 dz$$
$$ \frac{\partial L}{\partial w_2} = dw_2 = x_2 dz$$
$db = dz$
그리고 여느 경사하강법처럼 파라미터는 동시에 다음과 같이 값이 갱신(update)됩니다.
$w_1 = w_1 - \alpha \partial w_1$
$w_2 = w_2 - \alpha \partial w_2$
$b = b- \alpha \partial b$
Gradient Descent on m Examples
단일 샘플만 가지고 경사하강법을 고민해봤는데, 이제는 m개의 전체 train 데이터에 대해서 cost function을 계산할 경우의 경사하강법을 고민해보고자 합니다.
Cost function은 loss function에서 summation과 m으로 나누기가 값에 붙었었죠.
$$J(w,b) = \frac{1}{m} \sum_{i=1}^{m}L(a^{(i)}, y) $$
$$a^{(i)} = \hat y^{(i)} = \sigma(z^{(i)}) = \sigma(w^Tx^{(i)}+b)$$
경사하강법에서 파라미터가 업데이트되는 방식을 그대로 갖고 오되, 전체 데이터의 합 그리고 m으로 나눠줌으로써 평균을 구하는 것이 전체 데이터에 대한 경사하강법입니다. 그리고 전체 데이터에 대해 파라미터가 각각 갱신(update)되는 과정을 냅다 코드 형태로 작성해서 보여주십니다.

위 코드를 통해 우리가 궁극적으로 경사하강법에서 업데이트하는 내용은 다음과 같습니다.
$$w_1 = w_1 - \alpha d w_1$$
$$w_2 = w_2 - \alpha d w_2$$
$$b = b - \alpha d b$$
이번 샘플 코드는 n=2 임을 가정했지만, n이 늘어나게 되면 추가적인 for문이 필요합니다. 이는 매우 비효율적이기 때문에 앞으로는 벡터화를 통해 코드를 단순화하는 방법을 알아보겠습니다.
Don't worry about that. -Andrew Ng 교수님의 한마디-
- 강의: https://youtu.be/eqEc66RFY0I



