Andrew Ng 교수님의 Machine Learning 강의를 정리한 내용입니다.
Multiple features (variables)
집값을 예측하기 위해서 집크기(size in feet^2)를 변수로 가지고 선형회귀분석을 진행했습니다. 변수로 방 갯수, 층수, 연식 값이 있다면 집값을 예측하는데 더 많은 정보를 가지게 되겠죠. 변수가 여러개다보니 $$x_1, x_2, x_3, x_4$$ 위와 같이 지정합니다. 해당 표기는 $$x_j$$로 j 번째 피처를 의미합니다.
$$\overrightarrow{x}^i$$ 가 가지는 의미는 모든 training 예제의 i번째 피처들 입니다. i번째 줄의 값들을 모두 일컫기 때문에 값이 하나가 아닌 여러개임을 나타내기 위해 행벡터라는 용어도 쓰인다고 합니다. 행벡터 안에 들어있는 j번째 값을 부르고 싶다면, $$x_j^i$$ 로 특정값을 소환시킬 수 있습니다.
변수가 여러개이기 때문에 이전 일차방정식 모델도 사용할 수 없습니다. 아래와 같이 변경될 수 있겠네요.
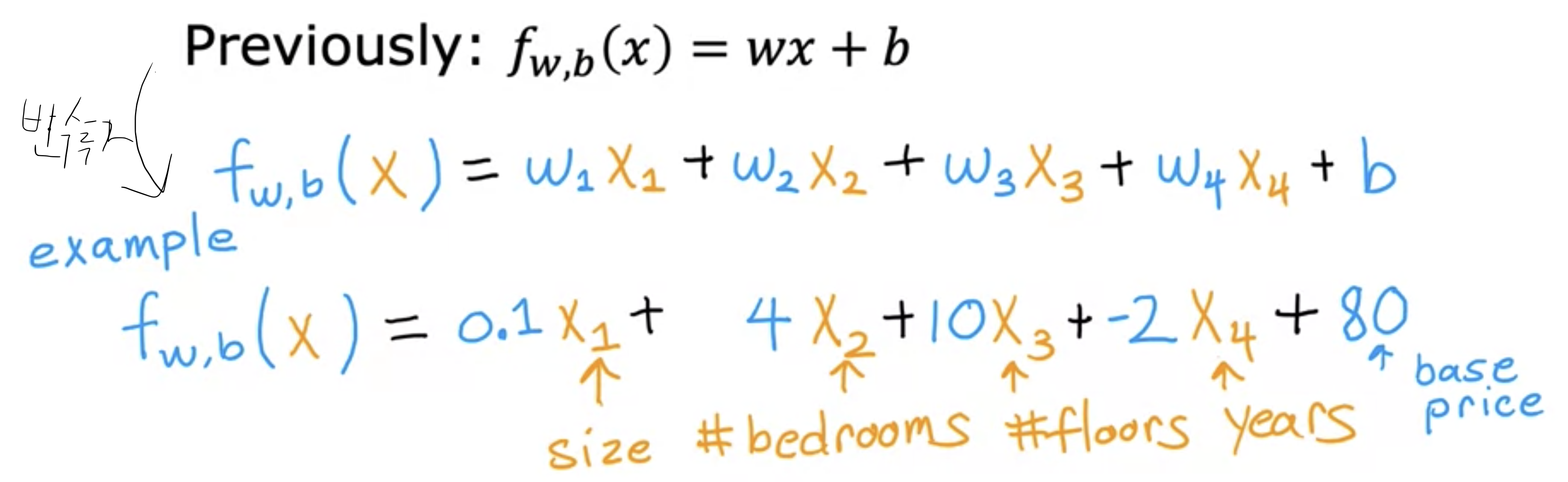
공식을 벡터로 표시하고 내적을 통해 줄이면 또 다음과 같이 줄일 수 있다고 합니다.

위와 같이 변수가 많은 선형회귀방정식을 다중선형회귀방정식 (multiple linear regression) 이라고 부릅니다. 다변량 회귀는 여기서 배우는게 아닌 다른 용어입니다.
Vectorization
벡터화를 사용하면 코드가 짧아지고 실행 효율도 훨씬 높아집니다. 또한 modern numerical linear algebra 라이브러리인 numpy와 GPU를 사용할 수 있습니다. 코드로는 매우 짧아지는 모습을 볼 수 있습니다.

실제 실행속도도 빨라지는데, Andrew Ng 교수님은 직접 벡터화된, 벡터화 안된 버전의 알고리즘을 작성해 구현해봤다고 합니다. 벡터화로 내적을 계산하는 방법은 행벡터 안의 값들을 병렬 (in parallel)로 동시에 계산하고 한번에 더한다고 합니다.
Gradient Descent for Multiple Regression
경사하강법에서 w를 업데이트하기 위해서는 w의 편미분 값을 learning rate와 곱해서 w에서 빼기를 진행했었습니다. w가 많아지게 되면서 업데이트해야 하는 w값, 업데이트를 하기 위해 계산해야 하는 편미분 값 (d)를 w갯수만큼 개산해야 합니다. 이 과정 또한 벡터의 병렬 계산을 통해 한번에 미분, 한번에 w값 업데이트가 가능합니다. 경사하강법 공식을 까먹었을 수 있으니 슬라이드 전체 캡쳐본을 첨부합니다.

이와 같이 병렬처리를 이용하여 w갯수가 몇개이던 효율적인 선형회귀를 구현할 수 있습니다.
위에서 사용한 $$J(w)$$ 의 편미분 기호에 직접 편미분 결과를 대입하면 다음과 같이 공식을 만들어낼 수 있습니다.

$$w_1 ... w_n$$ 과 같이 n개의 w를 각각 업데이트를 진행해야하는데, $$J(w_n)$$ 을 편미분한 부분 (위 이미지에서 노란색 형광펜 칠해진 부분)에 각각 업데이트할 $$x_n$$을 대입해줍니다.
Gradient Descent가 아닌 대체 가능한 normal equation
Gradient Descent가 cost function인 J(w)의 최소값을 찾는 훌륭한 공식이지만, 선형회귀에 한해서 normal equation을 사용할 수 있습니다. 경사하강법과 마찬가지로 cost function의 w, b의 값을 찾을 수 있지만, 반복하는 경사하강 알고리즘이 필요 없습니다. 대신 고급 선형 대수 라이브러리를 사용합니다. 단점으로 경사하강법과 달리 다른 알고리즘 (예. logistic regression, neural network)에 사용할 수 없습니다. 또한 피처 수가 커지면 속도가 느려지는 점도 있습니다. 이러한 단점으로 머신러닝 전문가가 normal equation을 직접 구현할 일은 없지만, 선형회귀를 구현하는 머신러닝 라이브러리를 호출해서 사용한다면 백단에서 normal equation을 사용하여 w,b 값을 찾아낼 수도 있습니다. 그렇지만 끝으로 Gradient Descent가 더 낫다 라고 강조합니다.
[생각]
해당 유튜브 영상의 댓글로 이렇게 수학적으로 풀어내는 것 말고 실제로 예측할 때 어떤 것을 의미하는지 알고싶다는 코멘트가 달렸네요. 저는 왜 공식을 유도해보는지는 모르겠지만, Andrew Ng 교수님이 필요에 따라 건너 뛰어도 된다고 말씀하셔서 일반인 대상으로 정말 필수적인것만 소개해주시는구나 생각이 들어서 머리에 넣어보려고 하고 있습니다. 또한 대학교 교수님들도 ML에 사용되는 식들을 적극적으로 소개해주시고, 유도까지해주시는 경우가 많기 때문에 알아야 하나보다 하고 더이상 생각하지 않습니다.
추가적으로 경사하강법 공식에는 편미분값이 들어갑니다. 영상에서 편의상 미분이라고 설명하는데 영어로 derivative 입니다. Andrew Ng 교수님이 derivative 단어를 100번은 이상 외친거 같은데 교수님이 뭉개서 발음하시는 걸 보곤 한국인인 저에게 발음이 진짜 어려울 것 같습니다.
그나저나 티스토리 마크다운에서 괄호는 왜 사용할 수 없을까요? 언젠가 괄호표현 문제를 해결해보겠습니다.
[출처]
- 강의: [[Machine Learning Specialization]](https://youtu.be/jXg0vU0y1ak?si=-xyzBYOsLdXgN0AV)
강의를 들으면서 필기한 내용이라 오타가 발생할 수 있습니다. 잘못된 내용은 피드백 환영합니다.



