Andrew Ng 교수님의 Machine Learning 강의를 정리한 내용입니다.
앞선 강의에서 cost function은 training data를 설명하는 특정 파라미터들이 얼마나 적절한지 측정가능하게 했습니다. 측정가능하게 되면서 우리는 cost function에 따라 더 나은 파라미터를 결정할 수 있었습니다. 그러나 linear regression에서 사용했던 squared error는 logistic regression에 사용하기에 적합하지 않다고 합니다. 새로운 cost function에 대해 알아보시죠.
Cost Function for Logistic Regression
Logistic regression의 대표적인 예시 종양을 다시 데리고 나와보겠습니다. m개의 training samples이 있고, n개의 입력변수 x(종양 사이즈, 환자 나이 등)이 있으며, 출력변수인 y는 0 또는 1의 값을 가집니다. Logistic regression 모델의 방정식은 다음과 같습니다.
이 경우에 파라미터 w,b를 어떻게 선택해 방정식을 완성할 것이냐?가 저희의 궁극적인 목표입니다. Linear regression의 경우 mean squared error라는 cost function을 가졌었죠. Cost function을 그려보았을 때 그릇모양을 한 convex function이 나옵니다. 그리고 경사하강법으로 한걸음씩 강하하며, J(w,b)의 특정 값으로 수렴하는 최소점을 찾고자 했었습니다.
기존 MSE를 사용하게 되면, logistic regression의 경우 그릇 모양의 convex 그래프를 그리지 못합니다. non-convex이기 때문에 너무 많은 국소 최소값이 발생하게 됩니다. 따라서 다른 convex 모양의 함수를 정의해서 똑같이 경사하강법으로 global 최소점을 찾아야 합니다.

cost function J(w,b)에서 summation 안에 나누기 2까지 진행한 부분을 똑 떼어, 그 summation 안의 내용을 해당 training set의 Loss라고 이름을 붙이겠습니다. Loss를 따로 호출하면 입력 x를 통해 나온 f(x)와 실제값 y를 통해 대문자 L()로 로스를 다음과 같이 표현할 수 있습니다.

Logistic function에 동일한 Cost function J(w,b)를 적용하려고 했을 때, non-convex를 그린 것을 확인했으니 새로운 J(w,b)와 L() 함수를 구해보려고 합니다. 먼저 Loss function L()을 구해보겠습니다.

Logistic loss function은 위와 같이 정의할 수 있는데, y값이 무엇인지에 따라 Loss 함수의 정의가 달라지게 됩니다. 우리는 해당 Loss는 하나의 training example 에 대해서 예측을 잘하는지를 측정하는 것이고, 그것들을 합쳐서 전체 데이터에 대해 잘 예측하고 있는지는 cost function으로 측정하고자 한다는 점을 생각해야 합니다.
실제 y값을 기준으로 Loss function을 나누고, log함수를 그렸을 때, 적절한 Loss function이 그려지는 것을 확인할 수 있습니다. 먼저 y=1인 경우의 그래프 살펴보겠습니다. y=1 인 경우 로그함수가 upsidedown으로 뒤집혀진 그래프입니다.(파란색 그래프)

그렇지만 log함수에 들어가는 값인 f(x)를 0 또는 1로 계산하고자 하는 것이 Logistic regression이므로 가로축이 0과 1인 부분만 똑 떼어내서 보면 아래 그림과 같습니다.

예측값 f(x)를 정답인 1과 가까이 계산할 경우 손실 Loss가 적겠고, 1과 먼 0.1로 계산했을 경우, 반대를 10% 확률로 잘못 예측한 수준이 아니라 어마어마하게 큰 Loss를 가지게 됩니다. 이와 같은 손실을 계산을 통해 실제 y값에 가까운 f(x)를 구하기 위해 알고리즘을 업데이트할 수 있겠죠.
y=0인 경우의 손실함수를 살펴보겠습니다. 그려지는 그래프 모양은 다음과 같습니다.(파란색 그래프)

y=0일 경우, y=1일 때와 반대로 1과 가까이 예측했을 때, 무한대에 가까운 Loss값을 가지게 되고, 0으로 예측했을 때 가장 작은 Loss값을 가지게 됩니다.
이렇게 Logistic regression에 새로운 Loss function을 구해줬고, 이는 전체 Cost function을 convex하게 만들기 때문에 우리는 경사하강법으로 함수의 global 최솟값을 찾을 수 있을 것입니다. 또한 앞서 평균구할 때 사용하는 Loss function의 전체 합 summation과 데이터 갯수만큼으로 나누기 두 가지를 Loss functrion 바깥으로 빼주었기 때문에 각각의 Cost function를 최소화하는 w,b를 찾는다면, 데이터 전체를 통틀어 적절한 파라미터를 찾는 것일 겁니다.
Simplified Cost Function
앞서 Loss Function을 살펴보았는데 조금 복잡해 보였죠? Logistic regression 모델의 파라미터에 맞게 경사하강법을 구현할 때 보다 간단하게 작성할 수 있다고 합니다. y는 1 또는 0 값을 가지므로 다음과 같이 하나의 식으로 정리할 수 있겠네요.

y값에 1을 대입해보면, y가 0일 때 작성했던 log함수 항이 날라가는 것을 간단하게 확인할 수 있습니다. 이와 같이 단순화된 Loss function을 가지고 Cost function도 작성해보겠습니다. Cost function은 전체 데이터의 Loss function의 평균이었습니다. 위 Loss function을 대입하고, 음수를 밖으로 빼면 아래 공식과 같이 도출할 수 있습니다.
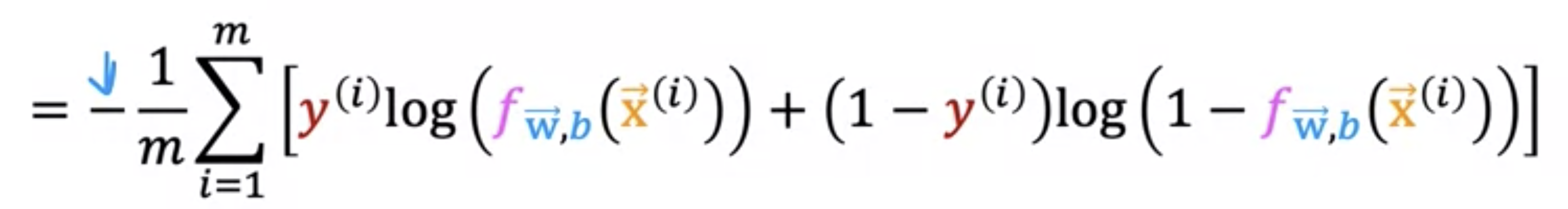
다른 Cost function도 많을 텐데 왜 하필 이거냐 라고 질문하는 이들에게 Andrew Ng 교수님은 이 강의에선 다룰 수 없겠다 라고 하셨습니다. 그러나 maximum likelihood라는 통계적 원리를 사용하여 다양한 모델에서 매개변수를 효율적으로 찾는 방식이라고 합니다. 결국 우리에게 중요한 것은 Cost function이 볼록 convex하냐 였고, 위 함수는 convex하다는 점에서 적절합니다.
다음편 예고: Logistic regression에 경사하강법 적용해보자~
[오타 발견]

- 자막에 달린 1.5는 오타로 보여 코세라에 리포팅했습니다. 실제 교수님은 one half라고 발음하셨고, 1/2을 의미하시는 것으로 보입니다. 리포팅에 대한 피드백이 오면, 글 수정하겠습니다.
[출처]



